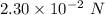Answer:
(a)
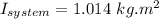
(b)
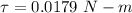
Solution:
As per the question:
Mass of the object, m = 1.30 kg
Length of the rod, L = 0.780 m
Angular speed,
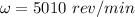
Now,
(a) To calculate the rotational inertia of the system about the axis of rotation:
Since, the rod is mass less, the moment of inertia of the rotating system and that of the object about the rotation axis will be equal:
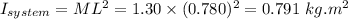
(b) To calculate the applied torque required for the system to rotate at constant speed:
Drag Force, F =