Answer:
(a)
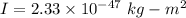
(b)

Step-by-step explanation:
It is given that,
The rotational inertia of a molecule,
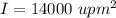
Angular velocity of the molecule,
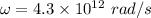
(a) The molecular weight of a molecule is measured in amu or u.
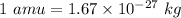
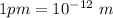
The rotational inertia of the molecule,
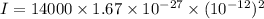
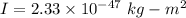
(b) The rotational kinetic energy of the molecule is given by :
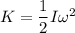
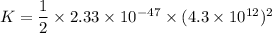
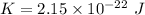
Since,
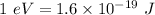
So,

Hence, this is the required solution.