Question

Ch11 problem # 62

In a very large closed tank the absolute pressure of teh airabove
the water is 6.01x 10^5 pa. The water leaves the bottom ofthe tank
through a nozzle that is directed straight upward. Theopening of
the nozzleis 4.00m below the suface of the water.(a) Find the speed
at which the water leaves the nozzle. (b)Ignoring the air
resistance and viscous effect, determie the heightto which the
water rises.

Answer 1

a) v₂ = 32.83 m / s, b) y = 54.99 m

Step-by-step explanation:

a) For this problem we must use Bernoulli's equation, we define the point as the surface of the water in the tank and point 2 is the point of the nozzle

P₁ + ½ ρ v₁² +ρ g y₁ = P₂ + ½ρ v₂² + ρ g y₂

As the nozzle is open to the outside it has the atmospheric pressure (P₂ =
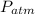`P_(atm)`) and the height y₂ = -4.00 m, since the tank is very large the water velocity inside the tank is very small, we will assume zero (v₁ = 0), replace

P₁ + ρ g (y₁-y₂) =
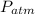`P_(atm)` + ½ ρ v₂²

v₂² = 2 /ρ [(P₁ -
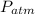`P_(atm)`) + ρ g (0 - y₂)]

Let's calculate

v₂² = 2/1000 [(6.01 -1.013) 10⁵ + 1000 9.8 4]

v₂ = √ (2 10⁻³ [4,997 10⁵ + 3.92 10⁴]) = √ 1077.8

v₂ = 32.83 m / s

b) the height at which the water reaches can be found with kinematics at this point the speed is zero

Vy² = v₂² - 2 g y

vy = 0

y = v₂² / 2g

Let's calculate

y = 32.83²/2 9.8

y = 54.99 m