Question

2. Sean has 56 songs on his MP3 player. He wants to randomly select 6 of the songs to use in a school project. How

many different groups of 6 songs could Sean select? Did you calculate the number of permutations or the number
of combinations to get your answer? Why did you make this choice?

Answer 1

Answer: The required number of different groups is 32468436 and it is calculated by the number of combinations because position of songs does not matter.

Step-by-step explanation: Given that Sean has 56 songs on his MP3 player and he wants to randomly select 6 of the songs to use in a school project.

We are to find the number of different groups of 6 songs that could Sean select.

Since Sean needs 6 different groups of songs, so the position of the songs do not matter. That is, we will use combination here.

Therefore, the number of different groups of 6 songs is

`^(56)C_6=(56!)/(6!(56-6)!)=(56*55*54*53*52*50)/(6*5*4*3*2*1)=32468436.`

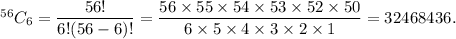
Thus, the required number of different groups is 32468436 and it is calculated by the number of combinations because position of songs does not matter.