Question

A 20 Kg satellite has a circular orbit with a radius of

8.0*10^6 m and a period of 2.4 h around a planet of unknown mass.
ifthe magnitude of the gravitational acceleration on the surface
ofthe planet is 8.0m/s^2, what is the radius of the planet?

Answer 1

Radius of the planet,
`r=5.8* 10^6\ m`

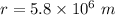
Step-by-step explanation:

It is given that,

Mass of the satellite, m = 20 kg

Radius of the circular orbit,
`r=8* 10^6\ m`

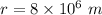
Time period of the motion of satellite,
`T=2.4\ h=8640\ s`

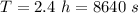
The acceleration on the surface of the planet is,
`a=8\ m/s^2`

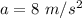
The relation between the time period of the satellite and its radius is given by third law of Kepler as :

`T^2=(4\pi^2)/(GM)r^3`

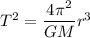
M is the mass of planet

`M=(4\pi^2r^3)/(T^2G)`

`M=(4\pi^2* (8* 10^6)^3)/((8640)^2* 6.67* 10^(-11))`

`M=4.059* 10^(24)\ Kg`

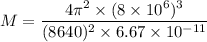
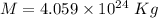
The acceleration on the surface of planet is given by :

`a=(GM)/(r^2)`

`r=\sqrt{(GM)/(a)}`

`r=\sqrt{(6.67* 10^(-11)* 4.059* 10^(24))/(8)}`

`r=5.8* 10^6\ m`

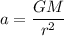
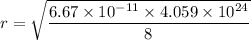
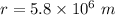
So, the radius of the planet is
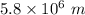`5.8* 10^6\ m`. Hence, this is the required solution.