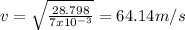Question

A copper

wire,whose cross-sectional area is 1.1 x 10-6
m2has a linear density of 7.0 x 10-3 kg/m and
is sturngbetween two walls. At the ambient temperature,
atransverse wave travels with a speed of 46 m/s on
thiswire. The coefficient of
linearexapansion for copper is 17 x
10-6(C)-1 and Young's modulus for copperis
1.1 x 1011 N/m2. What will be the speed of the wave
whenthe temperature is lowered by 14 C? Ignore any changein
the linear density caused by the change in temperature.

Answer 1

v = 64.14 m/s

Step-by-step explanation:

First we are going to calculate the initial tension force in the wire.

How:

`V = \sqrt{(T)/(\mu) }`

Where v: Wave's speed

T. Tension force

μ: Linear densityof the wire

Then:

`T = V^(2)\mu`

`T = 46^(2)(7 x 10^(-3)) = 0.322N`

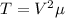
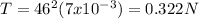
Now we calculate the linear dilation of the copper, thus

ΔL = αLoΔT

Where α:The coefficient of linear expansion for copper

ΔL =
`(17x10^(-6))( Lo)(-14) = 0.000238 Lo`

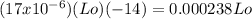
The Young's modulus is defined like:

`E = (TLo)/(A\Delta L)`

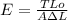
Where E : The Young's modulus

A: cross-sectional area

Then

`T = (EA\Delta L)/(Lo)`

`T = (1.1 x10^(11) (1.1x10^(-6) )(0.000238Lo))/(Lo) =28.798 N`

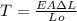
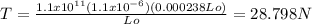
and the speed of the wave when the temperature is lowered is:

`v = \sqrt{(28.798)/(7x10^(-3) ) } = 64.14 m/s`