Question

What is the phase angle for a series RLC circuit containing

a50-W resistor,
a10-mF capacitor, and
a0.45-H inductor, when connected to a 60-Hz power supply?

Answer 1

To solve this problem we will apply the concepts related to angular frequency, which can be calculated with the given frequency. In turn, with this frequency you can calculate the capacitive reactance and inductive reactance. The angle phase depends on the tangent of these two variables. So if we have that,

`R = 50\Omega\\L = 0.45H\\C = 10*10^(-3)F \\f = 60 Hz \rightarrow V_(rms) = 120V`

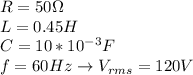
The angular frequency,

`\omega = 2\pi f \\\omega = 2\pi (60Hz)\\\omega = 376.99rad/s`

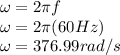
The capacitive reactance

`X_c = (1)/(\omega C)`

`X_c = (1)/((376.99rad/s)(10*10^(-3)F))`

`X_c = 0.2652 \Omega`

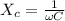
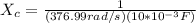
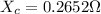
Inductive reactance

`X_l = \omega L`

`X_l = 376.99*0.45 = 169.6455\Omega`

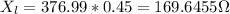
Phase angle is equal to

`\phi = tan^(-1) ((X_l-X_c)/(R))`

`\phi = tan^(-1) ((0.2652 -169.6455)/(100))`

`\phi = -59.4\°`

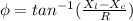
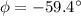
Since the phase angle is negative, the circuit is purely capacitive and the current leads the voltage by angle 59.4°