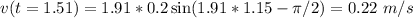Question

A small block is attached to an ideal spring and is moving in SHM on a horizontal, frictionless surface. The amplitude of the motion is 0.200 mm and the period is 3.28 ss .

Part A
What is the acceleration of the block when x= 0.160m ?
Express your answer with the appropriate units.

Part B
What is the speed of the block when x= 0.160m ?
Express your answer with the appropriate units

Answer 1

a = -0.59 m/s^2

v = 0.22 m/s

Step-by-step explanation:

The equation of motion in simple harmonic motion is defined as

`x(t) = A\cos(\omega t - \phi)`

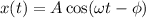
where A is the amplitude, ω is the angular frequency, and Ф is the phase angle which has to be determined by initial conditions.

The period of the motion is given, so the angular frequency could be calculated.

`\omega = 2\pi f = 2\pi (1)/(T) = 2*3.14*(1/3.28) = 1.91`

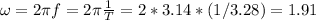
The initial conditions are not given in the question, so I will assume that at t = 0, the block is at the origin (x = 0). (This assumption will not affect our final result, we can as well choose another initial point.)

`x(t=0) = 0 = 0.2\cos(1.91*0 - \phi)\\\cos(\phi) = 0\\\phi = \pi/2`

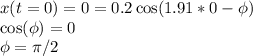
Let’s find the time when x = 0.160 m.

`0.16 = 0.2\cos(1.91t - \pi/2)\\1.91t - \pi/2 = 0.6435\\1.91t = 0.6435 + 1.5708 = 2.2143\\t = 1.15~s`

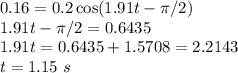
The velocity function is the derivative of the position function with respect to time.

`v(t) = (dx(t))/(dt) = -\omega A\sin(\omega t - \phi)`

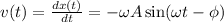
Similarly, the acceleration function is the derivative of velocity function with respect to time.

`a(t) = -\omega^2A\cos(\omega t - \phi)`

A)
`a(t = 1.15) = -(1.91)^2 0.2 \cos(1.91*1.15 - \pi/2) = -0.59~m/s^2`

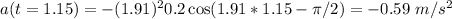
B)
`v(t = 1.51) = 1.91*0.2\sin(1.91*1.15 - \pi/2) = 0.22~m/s`