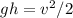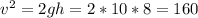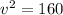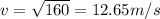Question

A roller coaster starts from rest at the top ofan 18m hill.

The car travels to the bottom of the hill andcontinues up the next
hill that is 10.0m high. How fast is the carmovings at the top of
the 10.0m hill if friction isignored?

Answer 1

12.65 m/s

Step-by-step explanation:

When friction is ignored, if the car travels from 18m hill to the bottom of the hill, afterwards it travels up to a 10m hill, then overall it has traveled a distance of 18 - 10 = 8 m vertically.

If the car starts from rest, then its potential energy is converted to kinetic energy:

`E_p = E_k`

`mgh = mv^2/2`

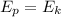
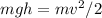
where m is the car mass and h is the vertical distance traveled, v is the car velocity at 10m hill

Let g = 10m/s^2. We can cancel m from both sides of the equation:

`gh = v^2/2`

`v^2 = 2gh = 2*10*8 = 160`

`v^2 = 160`

`v = √(160) = 12.65 m/s`