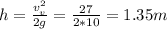Question

A water skier lets go of the tow rope upon leaving the end ofa

jump ramp at a speed of 14.0 m/s. The skier has a speed of 13.0m/s
at the highest point of the jump. Ignoring air resistance,determine
the skier's height H above the tope of the ramp at thehighest
point.

Answer 1

1.35m

Step-by-step explanation:

At the highest point of the jump, the vertical speed of the skier should be 0. So the 13m/s speed is horizontal, this speed stays the same from the jumping point to the highest point. The 14m/s speed at jumping point is the combination of both vertical and horizontal speeds.

The vertical speed at the jumping point can be computed:

`v_v^2 + v_h^2 = v^2`

`v_v^2 + 13^2 = 14^2`

`v_v^2 = 196 - 169 = 27`

`v_v = √(27) = 5.2 m/s`

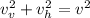
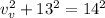
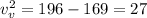
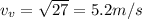
When the skier jumps to the its potential energy is converted to kinetic energy:

`E_p = E_k`

`mgh = mv_v^2/2`

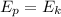
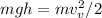
where m is the skier mass and h is the vertical distance traveled,
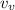`v_v` is the vertical velocity at jumping point, and h is the highest point.

Let g = 10m/s2

We can divide both sides of the equation by m:

`gh = v_v^2/2`

`h = (v_v^2)/(2g) = (27)/(2*10) = 1.35 m`