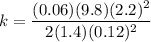Question

A small ball with a mass of 60.0 g is loaded into a spring gun,

compressingthe spring by 12.0 cm. When thetrigger is pressed the
ball emerges horizontally from the barrel ata height of 1.40 m
above the floor. Itthen strikes the floor after traveling a
horizontal distance of2.20 m. Use g = 9.80 m/s2.Assuming
all the energy stored in the spring is transferred to theball,
determine the spring constant of the spring.

Answer 1

K=70.58 Nw/m

Step-by-step explanation:

Conservation Of The Energy

When no losses are considered, like friction or air resistance, the total energy present in a system is constant. Three types of energy are commonly used in simple physics applications:

Kinetic energy:

`\displaystyle K=(mv^2)/(2)`

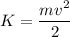
Potential gravitational energy:

`U=mgh`

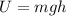
Elastic potential energy

`\displaystyle P=(kx^2)/(2)`

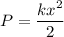
The variables used in the formulas are: m=mass, v=speed, h=height above ground, g=acceleration of gravity, k=spring constant, x=spring compression

When the spring is compressed, the ball is at rest, and only two energies are present, the elastic and the potential. Thus

`E_o=P+U`

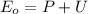
After the trigger is pressed, all the elastic energy is released and transformed in kinetic and the ball is fired at speed
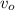`v_o`. At this moment, the ball has two energies: Kinetic and potential. The potential energy is the same as before because the ball is still at the same height, so

`E_1=K+U`

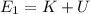
Equating both energies

`P+U=K+U`

`P=K`

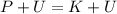
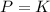
Or equivalently

`\displaystyle (kx^2)/(2)=(mv_o^2)/(2)`

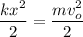
Rearranging

`kx^2=mv_o^2`

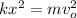
Solving for k

`\displaystyle k=(mv_o^2)/(x^2).......[1]`

We need to find
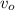`v_o` by using motion conditions. We know the ball reaches a distance d=2.2 m after traveling height of h=1.4 m. We can use these data to find
`v_o`.

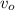The horizontal distance is given by

`d=v_o.t..........[2]`

The vertical height is

`\displaystyle h=(gt^2)/(2)...........[3]`

Solving for t in [2]

`\displaystyle t=(d)/(v_o)`

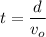
Replacing in [3]

`\displaystyle h=(g\left ( (d)/(v_o) \right )^2)/(2)`

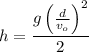
Operating

`\displaystyle h=(gd^2)/(2v_o^2)`

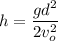
Solving for
`v_o^2`

`\displaystyle v_o^2=(gd^2)/(2h)`

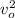
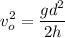
Replacing in [1]

`\displaystyle k=(m(gd^2)/(2h))/(x^2)`

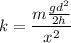
Rearranging

`\displaystyle k=(mgd^2)/(2hx^2)`

Computing with m=60 gr= 0.06 Kg, x=12 cm = 0.12 m

`\displaystyle k=((0.06)(9.8)(2.2)^2)/(2(1.4)(0.12)^2)`

`\boxed{K=70.58\ Nw/m}`