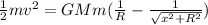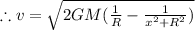Question

QuestionDetails:

Several planets (Jupiter, Saturn,Uranus) possess nearly
circular surrounding rings, perhaps composedof material that failed
to form a satellite. In addition,many galaxies contain ring-like
structures. Consider ahomogeneous ring of mass M and radius
R.
a.)What gravitational attractiondoes it exert on a
particle of mass m located a distance x from thecenter of the ring
along its axis?
b.) Supposes the particle falls fromrest as a result of
the attraction of the ring of matter. Find an expression for the
speed with which it passes through thecenter of the
ring.

Answer 1

To solve the two parts of this problem, we will begin by considering the expressions given for gravitational potential energy and finally kinetic energy (to find velocity). From the potential energy we will obtain its derivative that is equivalent to the Force of gravitational attraction. We will start considering that all the points on the ring are same distance:

`r = √(x^2+R^2)`

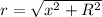
Then the potential energy is

`U = (-GMm)/(√(x^2+R^2))`

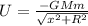
PART A) The force is excepted to be along x-axis.

Therefore we take a derivative of U with respect to x.

`F = -(dU)/(dx)`

`F = -(d)/(dx)(GMm((1)/(R)-(1)/(√(x^2+R^2))))`

`F = (GMmx)/((x^2+R^2)^(3/2))`

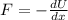
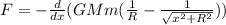
This expression is the resultant magnitude of the Force F.

PART B) The magnitude of loss in potential energy as the particle falls to the center

`U = GMm((1)/(R)-(1)/(√(x^2+R^2)))`

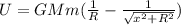
According to conservation of energy,

`(1)/(2)mv^2 = GMm ((1)/(R)-(1)/(√(x^2+R^2)))`

`\therefore v = \sqrt{2GM((1)/(R)-(1)/(x^2+R^2))}`