Question

PLEASE HELP I NEED THIS FAST

Which equation models the linear relationship in the table below?

Answer 1

The correct answer is option A)
`\(y = -3x - 2\)`.

To find the equation that models the linear relationship in the given table, we can use the slope-intercept form
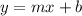`\(y = mx + b\)`, where
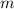`\(m\)` is the slope and
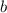`\(b\)` is the y-intercept. We'll calculate the slope using two points from the table.

Let's use the points (-4, 10) and (1, -5):

`\[m = \frac{\text{change in } y}{\text{change in } x} = (-5 - 10)/(1 - (-4)) = (-15)/(5) = -3.\]`

Now that we have the slope
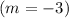`(\(m = -3\))`, we can choose the correct equation from the options. Since the slope is negative, the correct equation should have a negative coefficient for
`\(x\)`.

Comparing the options, the correct equation is
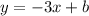`\(y = -3x + b\)`. To find
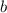`\(b\)`, we can use one of the points from the table, for example, (-4, 10):

`\[10 = -3(-4) + b \implies 10 = 12 + b \implies b = -2.\]`

Therefore, the equation that models the linear relationship in the table is
`\(y = -3x - 2\)`, which corresponds to option A.

The question probable maybe:

Which equation models the linear relationship in the table below?
| x | y |

|-------|-------|

| -4 | 10 |

| 1 | -5 |

| 6 | -20 |

|-------|-------|
A. y=-3x-2
B. y=-3x+22

C. y=3x-2

D. y=3x+22