Question

Surviving a ship wreck, what is the minimum mass of wood (density 60% that of sea water) necessary to support a 70kg woman standing on a block of wood floating in the water?

Answer 1

To solve this problem we will apply the concepts related to the principle of archimedes. for which we will summarize that the bearing force must be equivalent to the mass of the individual and the mass of the way. Said mass of wood will be expressed in terms of density and volume. Finally with the values found we will proceed to find the Volume of the wood and thus find the mass.

`(M_(woman)+M_(wood))g=F_B`

`(M_(woman)+M_(wood))g=V\rho_(water) g`

`(M_(woman)+V \rho_(wood))g=V\rho_(water) g`

`(M_(woman)+V \rho_(wood))=V\rho_(water)`

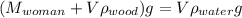
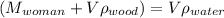
For the relation between density and Volume we have that,

`mass=density* volume`

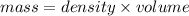
Where given that,

Mass of woman,
`M_(man)=70kg`

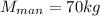
If the density of the wood is 60% the density of the water we will have to

Density of water,
`\rho_(water)=1000kg/m^(3)`

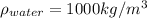
And density of wood is

`\rho_(wood)=600kg/m^(3)`

Now the mass of the man can be expressed as

`M_(woman)=V\rho_(water) -V\rho_(wood)`

`V=(M_(woman))/(\rho_(water) -\rho_(wood))=(70\;kg)/(1000\;kg/m^(3)-600\;kg/m^(3))`

`V=0.175m^(3)`

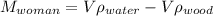
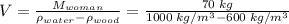
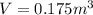
Mass of wood required is given by,

`M_(wood)=V\rho_(wood)=0.175m^(3)*600kg/m^(3)`

`\mathbf{\therefore M_(wood)=105kg}`

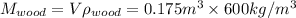
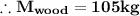
Therefore the minimum mass necessary to support a 70kg Woman is 105Kg.