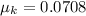Question

A 2.00 kg block situated on a rough incline is connected to aspring

of negligible mass having a spring constant of 100 N/m (Fig.P5.76).
The block is released from rest when the spring isunstretched, and
the pulley is frictionless. The block moves21.4 cm down the incline
before comingto rest. Find the coefficient of kinetic friction
between the blockand incline.

Answer 1

To find the coefficient of kinetic friction between the block and incline, we can use the concepts of work and energy. First, calculate the work done by the spring and then calculate the work done by the friction force. Finally, you can use the equation f = u * N to solve for the coefficient of kinetic friction.

Step-by-step explanation:

To find the coefficient of kinetic friction between the block and incline, we can use the concepts of work and energy. First, we need to calculate the work done by the spring when the block moves 21.4 cm down the incline. This work is equal to the change in potential energy of the spring. The potential energy stored in the spring is given by the formula: PE = 1/2kx^2, where PE is the potential energy, k is the spring constant, and x is the displacement from the equilibrium position. In this case, the displacement is 21.4 cm, which is 0.214 m. The work done by the spring is then given by the formula: W = -PE = -1/2kx^2. Plugging in the values for k and x, we get: W = -1/2 * 100 N/m * (0.214 m)^2 = -2.294 J.

Next, we can calculate the work done by the friction force when the block moves down the incline. This work is equal to the change in kinetic energy of the block. The kinetic energy of the block is given by the formula: KE = 1/2mv^2, where KE is the kinetic energy, m is the mass of the block, and v is the velocity. Since the block comes to rest, its final velocity is 0. The initial velocity can be calculated using the formula: v = sqrt(2gh), where g is the acceleration due to gravity and h is the height of the incline. The height of the incline can be calculated using the formula: h = x sin(theta), where theta is the angle of the incline. Plugging in the values, we get: h = 0.214 m * sin(30°) = 0.107 m. The initial velocity is then: v = sqrt(2 * 9.8 m/s^2 * 0.107 m) = 1.47 m/s. The work done by friction is: W = KE = 1/2 * m * v^2 = 1/2 * 2 kg * (1.47 m/s)^2 = 2.15 J.

Now, we can calculate the coefficient of kinetic friction using the formula: f = u * N, where f is the frictional force, u is the coefficient of kinetic friction, and N is the normal force. The normal force can be calculated using the formula: N = m * g * cos(theta), where g is the acceleration due to gravity. Plugging in the values, we get: N = 2 kg * 9.8 m/s^2 * cos(30°) = 16.94 N. The frictional force is then: f = 4.86 N. Plugging in the values for f and N in the equation f = u * N, we can solve for u: u = f / N = 4.86 N / 16.94 N = 0.287.

Answer 2

Figure P5.76 is missing from this problem, but I found a similar problem whose figure I uploaded with this answer. The angle of the incline might be different though, but the procedure to follow is the same.

Answer:

`\mu_(k)=0.0708`

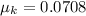
Step-by-step explanation:

In order to solve this problem we must first do a drawing of the situation so we can analyze it better. (See attached picture)

Once we have the drawing of the problem, we can go ahead and draw a free body diagram, which will help us determine what forces are acting upon the object. There are different approaches we can take to solve this problem, but I will use an energy balance to do so.

So first we do a sum of forces on the y-axis. This is for us to find what the Normal force is, which will be used to find the force of friction, so we get:

`\sum F_(y)=0`

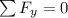
by looking at the free body diagram we get the sum of forces to be:

`N-W_(y)=0`

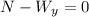
when solving for the normal force we get that:

`N=W_(y)`

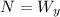
we also know from the free body diagram that:

`W_(y)=Wcos \theta`

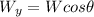
and

`W_(y)=mgcos \theta`

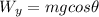
So:

`N=mgcos \theta`

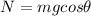
we can also determine the height of the block at the time it is released by analyzing the triangle find in the uploaded figure,, so we get that:

`sin(37^(o))=(h)/(21.4cm)`

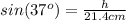
so:

h=21.4cm sin(37°)

h=12.88cm

Once we got this, we can go ahead and do an energy balance on the system, so we get that:

`U_(0)+K_(0)+E_(s0)=U_(f)+K_(f)+W_(f)+E_(sf)`

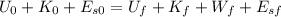
where:

U=potential energy

K=Kinetic energy

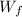`W_(f)`=Work of friction

`E_(s)`=Potential energy of the spring

Since the object is released from rest we know the initial kinetic energy is zero, just like the initial potential energy of the spring since when the block is released, the spring is unstretched. We also know the final potential energy of the block is zero because it reached its lowest point, while the kinetic energy of the block is also zero because it came to rest at that point. This simplifies our energy balance so we get:

`U_(0)=W_(f)+E_(sf)`

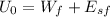
we can now determine each part of the equation so:

`U_(0)=mgh`

`W_(f)=fx`

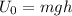
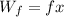
we know that friction is given gy the equation:

`f=\mu_(k)N`

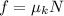
and that

`N=mgcos \theta`

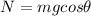
so:

`f=\mu_(k)mgcos \theta`

and

`W_(f)=\mu_(k)mgxcos \theta`

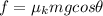
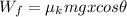
and finally:

`E_(s)=(1)/(2)kx^(2)`

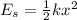
Once we got all these equations we can substitute them into our balance of energy, so we get:

`mgh=\mu_(k)mgx cos \theta + (1)/(2)kx^(2)`

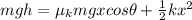
we can now solve this for
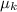`\mu_(k)` so we get:

`mgh - (1)/(2)kx^(2)=\mu_(k)mgx cos \theta`

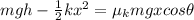
and:

`\mu_(k)=(2mgh-kx^(2))/(2mgxcos\theta)`

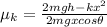
now we can substitute the given data, make sure to use the correct units:

`\mu_(k)=(2(2kg)(9.81m/s^(2))(12.88x10^(-2)m)-(100N/m)(21.4x10^(-2))^(2))/(2(2kg)(9.81m/s^(2))(21.4x10^(-2))cos(37^(o)))`

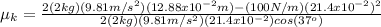
which solves to:

`\mu_(k)=0.0708`