Question

A solid cylindrical object has a mass of 2.0 kg, a diameter

of0.10m, and a length of 0.18m. What is the moment of inertiaof the
body about an axis along the axis of thecylinder?

Answer 1

I = 0.0025 kg.m²

Step-by-step explanation:

Given that

m= 2 kg

Diameter ,d= 0.1 m

Radius ,
`R=(d)/(2)`

`R=(0.1)/(2)`

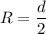
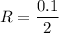
R=0.05 m

The moment of inertia of the cylinder about it's axis same as the disc and it is given as

`I=(mR^2)/(2)`

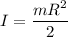
Now by putting the all values

`I=(2* 0.05^2)/(2)`

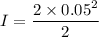
I = 0.0025 kg.m²

Therefore we can say that the moment of inertia of the cylinder will be 0.0025 kg.m².