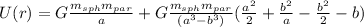Answer:
The sketch for the Gravitational force F and the potential energy U are attached to this answer.
Step-by-step explanation:
To obtain the gravitational force, we can consider the gravitational field GF(r) as:
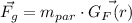
To calculate the gravitational field we can use the Gauss theorem. By considering a homogeneous mass of the sphere (constant density) and the spherical symmetry, we can determinate than the gravitational field direction is
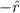 .
.
Considering a constant density:

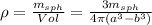
Applying a spherical gaussian surface for different radius r:
for R<b:
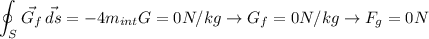
for b<R<a:
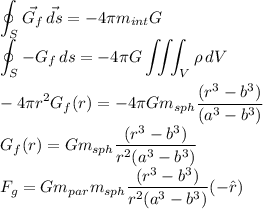
for a<R:
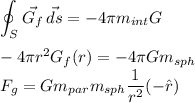
For the potential energy you can integrate the field to obtain the gravitational potential and the multiplying for the particle mass:
for a<R:
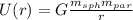
for b≤R≤a:
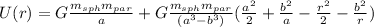
for R≤b: