Question

What is the maximum value of the magnetic field at a
distance2.5m from a 100-W light bulb?

Answer 1

To solve this problem we will apply the concepts related to the intensity included as the power transferred per unit area, where the area is the perpendicular plane in the direction of energy propagation.

Since the propagation occurs in an area of spherical figure we will have to

`I = (P)/(A)`

`I = (P)/(4\pi r^2)`

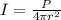
Replacing with the given power of the Bulb of 100W and the radius of 2.5m we have that

`I = (100)/(4\pi (2.5)^2)`

`I = 1.2738W/m^2`

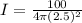
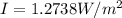
The relation between intensity I and
`E_(max)`

`I = (E_max^2)/(2\mu_0 c)`

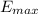
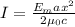
Here,

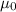`\mu_0` = Permeability constant

c = Speed of light

Rearranging for the Maximum Energy and substituting we have then,

`E_(max)^2 = 2I\mu_0 c`

`E_(max)=√(2I\mu_0 c )`

`E_(max) = 2(1.2738)(4\pi*10^(-7))(3*10^8)`

`E_(max) = 30.982 V/m`

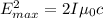
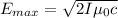
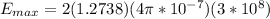
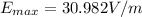
Finally the maximum magnetic field is given as the change in the Energy per light speed, that is,

`B_(max) = (E_(max))/(c)`

`B_(max) = (30.982 V /m)/(3*10^8)`

`B_(max) = 1.03275 *10{-7} T`

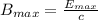
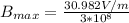
Therefore the maximum value of the magnetic field is
`B_(max) = 1.03275 *10{-7} T`