Answer:
No, the lengths of the diagonals cannot be 4 in and 3 in.
Explanation:
The parallelogram law which is also known as parallelogram identity states that the sum of the squares of the lengths of the four sides of a parallelogram equals the sum of the squares of the lengths of the two diagonals.
According to the law,In the following figure
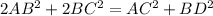 ----------------------(1)
----------------------(1)
In the question it is stated that,
one side is 5 inches. So lets assume AB = 5
The Diagonals are 4 and 3 inches
Let AC be 4 inches and BD be 3 inches
Substituting the given values in (1)
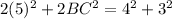
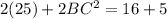
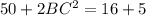
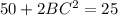
Now this is not possible and does not satisfy the parallelogram ,Thus the diagonals cannot be 3 inches and 4 inches