Answer:
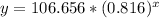
Explanation:
The exponential equation will be of the form:
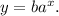
Now from the information give we have two points:
at
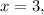
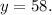
at
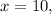
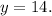
Thus we have two equations
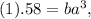
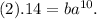
From equation
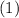 we solve for
we solve for
 :
:
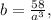
and put this value into equation
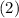 and we get:
and we get:
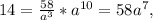
and solve for
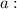
![a=\sqrt[7]{(14)/(58) }=0.8162.](https://img.qammunity.org/2021/formulas/mathematics/middle-school/rsfsnlcutvjpppuoisitothy4r1ua54vf7.png)
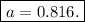
We now put this value into equation (1) and solve for
 :
:
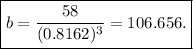 .
.
With values of
 and
and
 in hand, we have our exponential function:
in hand, we have our exponential function:
