Question

The high school soccer team can have no more than 26 players. Write and solve an inequality to determine how many more players can make the team if the coach has already chosen 17.

Answer 1

The inequality to determine how many more players can make the team is:

`x+17\leq 26`

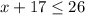
On solving it we get :
`x\leq 9`

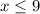
Thus, the number of players that can still make in the team must be no more than 9.

Explanation:

Given:

Maximum number of players the soccer team can have = 26

Number of players already chosen by coach = 17

To find how many players can still make the team.

Solution:

Let the players that can still make the team be =
`x`

Players already chosen = 17

Total number of players in the team can be given as =
`x+17`

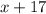
Total numbers must not exceed 26.

So, the inequality can be written as:

`x+17\leq 26`

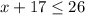
Solving for
`x`

Subtracting both sides by 17.

`x+17-17\leq 26-17`

∴
`x\leq 9`

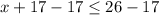
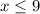
Therefore, no more than 9 players can still make in the soccer team.