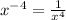1 Answer

Conspirisi · Answer 1 · 2021-09-10T10:09:27+0000

Answer:
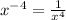
x^(-4)=(1)/(x^(4))

Explanation:

We have the following expression:

$(\sqrt[3]{x^(2)} \sqrt[6]{x^(4)})^(-3)$

Which can also be written as:

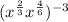
$(x^{(2)/(3)} x^{(4)/(6)})^(-3)$

Since we have exponents with the same base
inside the parenthesis, we can sum both exponents:

$(x^{(4)/(3)})^(-3)$

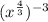
Now, we have to multiply the exponent out of the parenthesis with the inner exponent and have the following result:

x^(-4)=(1)/(x^(4))

Please log in or register to add a comment.