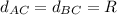Question

4.

a. Show that
(x − 2)(x − 6) + (y − 5)(y + 11) = 0
is the equation of a circle. What is the center of this circle? What is the radius of this circle?
b. A circle has diameter with endpoints (aa, ????????) and (cc, dd). Show that the equation of this circle can be
written as
(x − a)(x − c) + (y − ????)(y − d) = 0.

Answer 1

a)
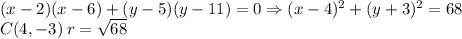`(x-2)(x-6) + (y-5)(y-11) =0\Rightarrow (x-4)^(2)+(y+3)^(2)=68\\C(4,-3) \:r=√(68)` b) (a,b) (c, d) As long as (a,b) and (c,d) are the endpoints of of the diameter.

Explanation:

a)

1) The reduced formula of the Circumference is given by:

`(x-a)^(2)}+(y-b)^(2)=r^(2)`

2) Let's expand the factored one into one closer to the pattern above:

`x^(2)-8x+12+y^(2)+6y-55=0\Rightarrow x^(2)-8x+y^(2)+6y=43`

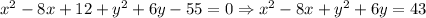
3) Completing the square for both trinomials:

`(x-4)^(2)+(y+3)^(2)=43+16+9\Rightarrow (x-4)^(2)+(y+3)^(2)=68`

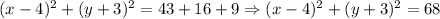
4) In the Reduced Formula,
`(x-a)^(2)}+(y-b)^(2)=r^(2)`,

`C(a,b) \Rightarrow C(4,-3) \:the\:radius\:is\:r=√(68) \Rightarrow r=2√(17)`

b) Using the previous example to show this:

When we factor this way

`(x-a)(x -c) + (y -b)(y-d) = 0`

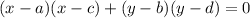
We are indeed, naming "a" and "b", the coordinates of (a, b) of the first endpoint and "b" and "d" the second endpoint as well.Id est, D (2, 5) and B (6,-11).

The radius, is
`√(68) \cong 8.25`

So yes, the equation of the circle can be written as

`(x-a)(x -c) + (y -b)(y-d) = 0`

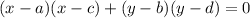
As long as (a,b) and (c,d) are the endpoints of of the diameter.

`d_(AC)=d_(BC)=R`