Answer:
A.
 ; B.
; B.
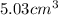 ; C. 19min
; C. 19min
Explanation:
First Step: Determine the size of the new straw
The size of the new straw is "double both the width and thickness of a standard straw". "A standard straw is 4mm in diameter and 0.5mm thick". So, the new straw is, then:
 or, equivalently,
or, equivalently,
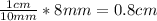 (Diameter).
(Diameter).
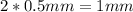 or, equivalently,
or, equivalently,
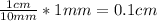 (Thickness).
(Thickness).
Second Step: Determine the cross-sectional area of the new straw
The cross-section area is "a section made by a plane cutting anything transversely, especially at right angles to the longest axis" Cross-section (2020), In Dictionary.com. Therefore, the area here is that of a circle:
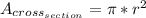 ,
,
Where
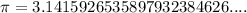 , and represents the ratio between a circle's circumference and its diameter, and r is the circle's radius or its diameter divided by 2.
, and represents the ratio between a circle's circumference and its diameter, and r is the circle's radius or its diameter divided by 2.
Then, the area is:
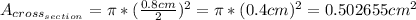 , rounded to the nearest hundredth:
, rounded to the nearest hundredth:
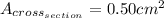
Third Step: Determine the maximum volume of milkshake that can be in the straw at one time
The new straw is 10cm long and its cross-section is, approximately,

Since the straw is a cylinder, and the volume of a cylinder is:
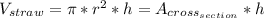 , where h is the height of the straw. In this case is 10cm long.
, where h is the height of the straw. In this case is 10cm long.
So, the maximum volume of milkshake that can be in the straw at one time is the volume of the straw:
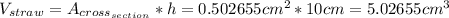 , rounded to the nearest hundredth:
, rounded to the nearest hundredth:
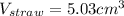
Fouth Step: Determine the minimum amount of time that it will take Corbin to drink the milkshake
A large milkshake is 950mL, and we know that:

So,
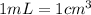 , therefore,
, therefore,
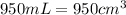
"Corbin withdraws the full capacity of a straw 10 times a minute" or Corbin withdraws:
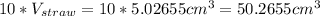 every minute.
every minute.
The large milkshake is
 . If Corbin withdraws
. If Corbin withdraws
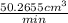 , the minimum amount of time that it will take him to drink the milkshake is:
, the minimum amount of time that it will take him to drink the milkshake is:
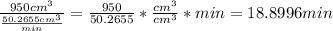 , since
, since
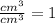 .
.
Rounded to the nearest minute, the minimum amount of time is 19min.