Question

The average of a list of integers goes up by 2 when 23 is added to the list. If 9 is added to the new list, then the average reduces by 1. How many integers were there in the original list?

Answer 1

There were 4 numbers in the original integer list.

Explanation:

Suppose that x is the sum of the integers in the original list, n is the number of integers in the original list and y is the average of those integers. The next formula represents the average of the numbers:

`y=(x)/(n)`

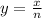
From this equation, you can tell that x=ny.

The problem gives us the following information:

1. The average of a list of integers goes up by 2 when 23 is added to the list, the next equation describes this situation (call this equation Eq 1)

`(x+23)/(n+1)=y+2`

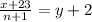
2. If 9 is added to the new list, then the average reduces by 1, the next equation describes this situation, you have to add 2 to n (call this equation Eq 2)

`(x+23+9)/(n+2)=y+2-1`

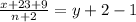
Now, use the fact that x=ny and replace it in both equations, the new equations will be:

Eq 1:

`(ny+23)/(n+1)=y+2`

`ny+23=(y+2)(n+1)`

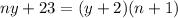
Eq 2:

`(ny+23+9)/(n+2)=y+2-1`

`ny+32=(y+1)(n+2)`

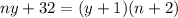
Solve y in Eq 1:

`ny+23=ny+y+2n+2\\ny-ny+23-2=y+2n\\y=21-2n`

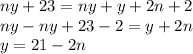
Replace y in Eq 2:

`n(21-2n)+32=((21-2n)+1)(n+2)\\21n-2n^2+32=(22-2n)(n+2)\\21n-2n^2+2n^2+32=22n+44-4n\\21n-22n+4n=44-32\\3n=12\\n=(12)/(3)\\n=4`

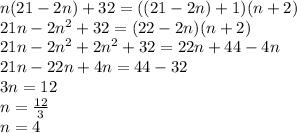
The number of integers in the original list (n) was 4.