Question

Of all of the rectangles with areas of 10 square units and with whole number side lengths, determine the dimensions of the rectangles with the greatest and least perimeter.

Answer 1

The dimension of rectangle will be 10 × 1 units with greatest perimeter 22 units and dimension of rectangle will 5 × 2 units with least perimeter 14 units.

Explanation:

Given:

Area of rectangle = 10 square units

We need to find the dimensions of the rectangles with the greatest and least perimeter.

Now we know that Area of rectangle is given by length times width.

Now 10 can be written as 10 × 1.

And also 10 can be written as 5 × 2.

Now If we consider dimension of rectangle as 10 × 1.

then length = 10 units

width = 1 units

then perimeter of rectangle is given by 2 times sum length and width.

perimeter of rectangle =
`2(10+1) =2* 11 =22 \ units`

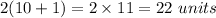
Now If we consider dimension of rectangle as 5 × 2.

then length = 5 units

width = 2 units

then perimeter of rectangle is given by 2 times sum length and width.

perimeter of rectangle =
`2(5+2) =2* 7 =14 \ units`.

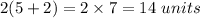Hence the dimension of rectangle will be 10 × 1 units with greatest perimeter 22 units and dimension of rectangle will 5 × 2 units with least perimeter 14 units.