Answer:
It would not be reasonable to say that more than half of the people with this disease would improve if they used the new drug
Explanation:
Data provided in the question:
Sample size, n = 1000
Number of people improved when they used the drug = 510
Thus,
Probability that Number of people improved when they used the drug
= 510 ÷ 1000
= 0.510
Now,
margin of error, E =

=
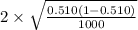
= 0.032 = 3.2%
Therefore,
Portion of 0.510 is likely to lie in the 3.2% of the actual value of population
And,
The lower portion can be as small as p - E
= 0.510 - 0.032
= 0.478 i.e 47.8% of the sample
Hence,
It would not be reasonable to say that more than half of the people with this disease would improve if they used the new drug