Question

5. Find an equation of a line through (−√2, ????) parallel to the line x − 7y = √5.

Answer 1

`y=(1)/(7)x+(√(5) )/(7)\:or\: y=0.14x+0.32`

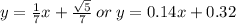
Explanation:

Hi there,

1) According to Analytical Geometry, parallel lines have the same slope. In this case:

`x-7y=\sqrt5 \Rightarrow-7y=\sqrt5-x \Rightarrow y=(√(5))/(7)+(x)/(7)`

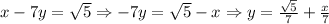
The slope is

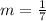`m=(1)/(7)` or
`m=0.14x`

2) Since we have the slope
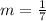`m=(1)/(7)` and one x coordinate: -1.41 (
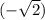`(-\sqrt2)` and the y-coordinate has not been given. Let's find precisely where this point is located at.

Plugging values.

`y=(√(5))/(7)+(1)/(7)(-√(2))\Rightarrow y=(2.25)/(7)+(1)/(7)*-1.41\:y=0.32-0.20\:y=0.12\\(-1.41,0.12)`

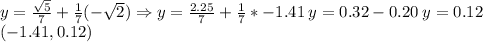
Finding 'b'

`0.12=0.14(-1.41)+b\\0.12=-0.20+b\\b=0.32`

3) Then

`y=(1)/(7)x+(√(5) )/(7)\:or\: y=0.14x+0.32`

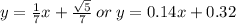
This equation is parallel to

`x-7y=\sqrt5 \Rightarrow y=0.14x-0.32`

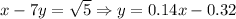
And the point

`(-\sqrt2, 0.12)`

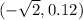
Graph:

Red line: Original equation given

Green one: parallel found.