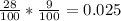Question

5. To prevent a flooded basement, a homeowner has installed two special pumps that work automatically and independently to pump water if the water level gets too high. One pump is

rather old and does not work 28% of the time, and the second pump is newer and does not work 9% of the time. Find the probability that both pumps will fail to work at the same time.

Answer 1

The probability that both pumps will fail to work at the same time is 0.025 or 2.5%.

Explanation:

The probability that both pumps will fail to work at the same time is the multiplication of the probabilities that the pomps fail.

That is

• the probability that the old pump fail =
  `(28)/(100)`

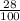
• the probability that the newer pump fail =
  `(9)/(100)`

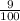
Then, the probability that both fail at the same time is:

`(28)/(100) * (9)/(100) = 0.025`