Answer:
There is no tangent line of the given circle at (6, 0).
Explanation:
Given equation of the circle,

∵ equation of a circle is
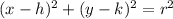 ,
,
Where, (h, k) is the center of the circle and r is the radius,
By comparing,
Center of the given circle = (0, 0),
Radius of the circle = 1 unit
Now, check whether point (6, 0) lie on the circle,
if x = 6,
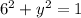
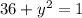
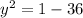
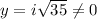
i.e., (6, 0) does not lie on the circle,
Hence, there is no tangent line of the given circle at (6, 0).