Question

1.

Find the exact solution to the equation.(2 points)

log base four of x equals two.

Answer 1

`x = 8^4`

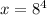
Explanation:

hey there,

< Here is what is given:

㏒
`_(8) x=4`

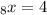
There's actually a lot of different ways you can remember this but the way I remember this is x is equal to 2nd to the power of last.

So 8 is the 2nd (since log is first), 4 is last (very last thing in the equation).

x = 8^4

You can use any of your own ways to remember this, but this is just my personal way. :) >

Hope this helped! Feel free to ask anything else.

Answer 2

x = 16

Explanation:

The equation is
`\log_(4) x = 2`

Now, converting this logarithmic equation into exponential equation, we get

`x = 4^(2) = 16` (Answer)

Alternate solution:

Given,
`\log_(4) x = 2`

⇒
`\log_(4)x = 2\log_(4)4`

{Since, we know that
`\log_(a)a = 1`}

⇒
`\log_(4)x = \log_(4)4^(2) = \log_(4)16`

{Since,
`a\log b = \log b^(a)` is a property of logarithm}

Cancelling log from both sides we get,

⇒ x = 16 (Answer)