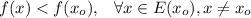Answer:
4
Explanation:
Let
 a function and
a function and
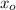 a point of the domain:
a point of the domain:
The function
 presents a relative maximum at
presents a relative maximum at
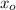 , when there exists an environment
, when there exists an environment
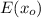 such that:
such that:
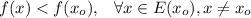
And the function
 presents a relative minimum at
presents a relative minimum at
 , when there exists an environment
, when there exists an environment
 such that:
such that:
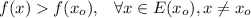
Necessary condition for the existence of extrema:
Let:
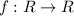
A function whose domain is
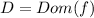 and
and
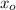 a point of the domain:
a point of the domain:
if
 reaches an extreme at
reaches an extreme at
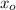 and
and
 is differentiable at
is differentiable at
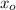 , then:
, then:
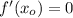
If we had the equation of the function we could find the extrema (maxima and minima) mathematically using the previous definition and other criteria. However since we only have the graph, we just can conclude that the maximum of the function is 4 based on this definition:
"The function
 presents a relative maximum at
presents a relative maximum at
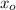 , when there exists an environment
, when there exists an environment
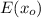 such that:"
such that:"