Question

6. Find the number of segments (chords) that can be drawn for each of the following:

a. 5 points on a circle
b. 6 points on a circle
c. 20 points on a circle
d. nn points on a circle

Answer 1

a) 10

b) 15

c) 190

d)
`{n \choose 2} = (n!)/((n-2)!2!)`

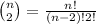
Explanation:

Lets start with the generic item (d). In order to draw a chord we need to pick two endpoints from the total of n points of the circle and draw the line between them. The total amount of lines we can draw is equivalent to the total pair of points we can pick to draw them.

In other words, we can draw as many chords as the amount of subsets of 2 elements we can pick from a set of n. That number is the combinatorial number of n with 2 given by

`{n \choose 2} = (n!)/((n-2)!2!)`

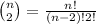
a) If n = 5, the answer is

`{5 \choose 2} = (5!)/((5-2)!2!) = (120)/(6*2) = 10`

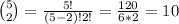
there are 10 possibilities

b) for n = 6

`{6 \choose 2} = (6!)/((6-2)!2!) = (720)/(24*2) = 15`

15 possibilities

c) for n = 20, we have

`{20 \choose 2} = (20!)/((20-2)!2!) = 190`

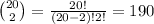
possibilities.

I hope that works for you!