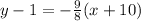Question

7. Kamal gives the following proof that y−1=8/9(x+10) is the equation of a line that is tangent to a circle given by

(x+1)^2+(y−9)2=145.
The circle has center (−1,9) and radius 12.04. The point (−10,1) is on the circle because (−10+1)^2+(1−9)^2=(−9)^2+(−8)^2=145.
The slope of the radius is 9 − 1/−1 + 10=89; therefore, the equation of the tangent line is y−1=8/9(x+10).
a. Kerry said that Kamal has made an error. What was Kamal’s error? Explain what he did wrong.
b. What should the equation for the tangent line be?

Answer 1

Answer with Step-by-step explanation:

We are given that equation of circle

`(x+1)^2+(y-9)^2=145=(√(145))^2`

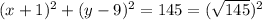
Compare with equation of circle

`(x-h)^2+(y-k)^2=r^2`

Where (h,k)=Center of circle

r=Radius of circle

We get circle of center=(-1,9)

Radius=12.04

The point (-10,1) is on the circle because it satisfied the circle equation .

Slope of radius=
`(1-9)/(-10+1)=(8)/(9)`

By using slope formula

Slope:
`m=(y_2-y_1)/(x_2-x_1)`

We know that radius is perpendicular to the tangent.

When two lines are perpendicular then their slope is opposite reciprocal to each other.

Slope of tangent=
`-(1)/((8)/(9))=-(9)/(8)`

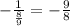
Now, the equation of tangent passing through the point(-10,1) with slope-9/8 is given by

`y-1=-(9)/(8)(x+10)`

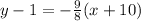
By using point-slope form

`y-y_1=m(x-x_1)`

a.Kamal has made an error to find the slope of tangent .

Slope of tangent=
`-(9)/(8)`

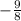
But he used slope of tangent 8/9

b.The equation of tangent line

`y-1=-(9)/(8)(x+10)`