Answer:
C. The 95% confidence interval is (0.2591, 0.3810). We are 95% confident that the true proportion of students attending the Spring Formal is between 25.91% and 38.10%.
Explanation:
The interpretation of a confidence interval at a x% confidence level if that we are x% sure that the true proportion(mean) of the population is in this interval.
Confidence interval
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence interval
, and a confidence interval
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.

In which
z is the zscore that has a pvalue of

For this problem, we have that:
Seventy-two of the 225 students said they would attend the Spring Formal. So
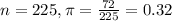
95% confidence interval
So
 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
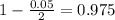 , so
, so
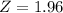 .
.
The lower limit of this interval is:

The upper limit of this interval is:
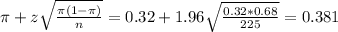
The correct answer is:
C. The 95% confidence interval is (0.2591, 0.3810). We are 95% confident that the true proportion of students attending the Spring Formal is between 25.91% and 38.10%.