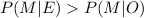Question

7. The claim that started this investigation was that students majoring in engineering are more likely to be in the marching band than students from other majors.

Describe the conditional probabilities that would be used to determine if this claim is accurate.

Answer 1

See explanation below.

`P(M|E) > P(M|O)`

Explanation:

Notation

First we need to define the following events:

E = The student is in a major of enginnering

O= The student is in a major different from enfinnering

M= The student is in the marching band

Solution for the problem

For this case we can calculate the following probability:

`P(M|E) =(P(M and E))/(P(E))`

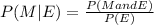
And that represent the following event: "Given a randomly selected student is an engineering major, what is the probability the student is in the marching band"

And the probability that need to calculate to compare is this one:

`P(M|O) =(P(M and O))/(P(O))`

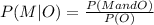
And that represent the following event: "Given a randomly selected student is NOT an engineering major, what is the probability the student is in the marching band"

And if the claim is satisfied we need to see this:

`P(M|E) > P(M|O)`