Incomplete Question the complete Question with figure is below.
Answer:
Therefore the length of line Segment BC is 20.5 in.
Explanation:
Given:
In Right Angle Triangle ABC
∠C = 90°
∠B = 35°
BC = a
AB = hypotenuse = 25
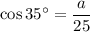
To Find:
BC = ?
Solution:
In Right Angle Triangle ABC , Using Cosine Identity we get
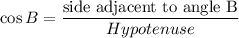
Substituting we get
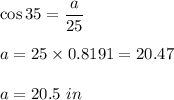
Therefore the length of line Segment BC is 20.5 in.