a)
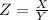 has CDF
has CDF
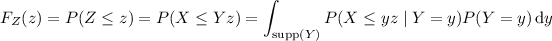
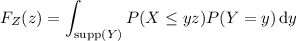
where the last equality follows from independence of
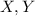 . In terms of the distribution and density functions of
. In terms of the distribution and density functions of
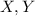 , this is
, this is
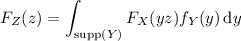
Then the density is obtained by differentiating with respect to
 ,
,
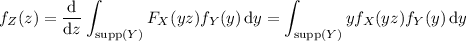
b)
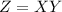 can be computed in the same way; it has CDF
can be computed in the same way; it has CDF
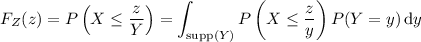
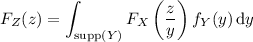
Differentiating gives the associated PDF,
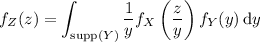
Assuming
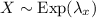 and
and
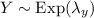 , we have
, we have
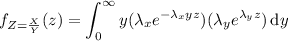
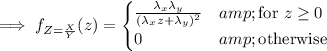
and
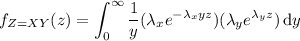
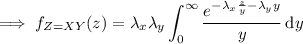
I wouldn't worry about evaluating this integral any further unless you know about the Bessel functions.