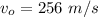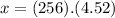Question

A fighter bomber is making a bombing run flying horizontally at 500 knots (256m/s) at an altitude of 100.0m.

a) How long will it take for the bomb to hit the ground after it is dropped from the plane?

b) How far will the bomb go over the ground (in the x direction) before it hits the target?

Answer 1

(a) t = 4.52 sec

(b) X = 1,156.49 m

Step-by-step explanation:

Horizontal Launching

If an object is launched horizontally, its initial speed is zero in the y-coordinate and the horizontal component of the velocity
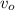`v_o` remains the same in time. The distance x is computed as .

`\displaystyle x=v_o.t`

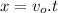
(a)

The vertical component of the velocity
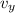`v_y` starts from zero and gradually starts to increase due to the acceleration of gravity as follows

`v_y=gt`

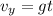
This means the vertical height is computed by

`\displaystyle h=h_o-(gt^2)/(2)`

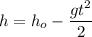
Where
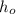`h_o` is the initial height. Our fighter bomber is 100 m high, so we can compute the time the bomb needs to reach the ground by solving the above equation for t knowing h=0

`\displaystyle t=\sqrt{(2h_o)/(g)}`

`\displaystyle t=\sqrt{(2(100))/(9.8)}=4.52\ sec`

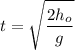
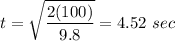
(b)

We now compute the horizontal distance knowing
`v_o=256\ m/s`

`\displaystyle x=(256).(4.52)`

`X=1,156.49\ m`