Question

8. Based on the multiplication rule for independent events, what is the probability of getting an airplane in both boxes? Explain your answer.

Answer 1

`P(A and B ) = (1)/(4)* (1)/(4)=(1)/(16)`

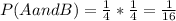
Explanation:

We assume the following problem: "Consider the following ways students might create their lists using the notation:

B for block, W for watch, R for ring, and A for airplane. The first letter represents the toy found in the first box, and the second letter represents the toy found in the second box. The first column represents getting the block in the first box, followed by each one of the other toys. The second column represents getting the watch in the first box, followed by each one of the other toys. The third column is developed with the ring in the first box, and the fourth column is developed with the airplane in the first box"

And the possible outcomes are:

BB WB RB AB

BW WW RW AW

BR WR RR AR

BA WA RA AA

As we can see we have 16 possibilities.

For this case if we use the independence of events we have the following rule. If A and B are independent events then:

`P(A and B) = P(A) *P(B)`

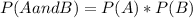
Let A = Select an airplane from the total of 4 for the first box

B= Select an airplane from the total of 4 for the second box

For this case probability of getting an airplane selected in the first box is 1 out of 4 since we have just one outcome possible and 4 possible.

`P(A) = (1)/(4)`

And the probability of getting an airplane selected in the second box is also 1/4 since for the first box selected we have the same number of optiosn for the second box , 4.

`P(B) = (1)/(4)`

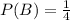
So then we have this:

`P(A and B ) = (1)/(4) (1)/(4)=(1)/(16)`