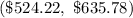Question

You want to rent an unfurnishedone-bedroom

apartment for next semester. The mean monthlyrent for a random
sample of 10 apartments advertised in the localnewspaper is $580.
Assume that the standard deviation is$90. Find a 95% confidence
interval for the mean monthly rentfor unfurnished one bedroom
apartments available for rent in thiscommunity.

Answer 1

Answer:
`(\$524.22,\ \$635.78)`

Explanation:

Confidence interval for population mean is given by :-

`\overline{x}\pm z^* (\sigma)/(√(n))`

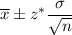
, where
`\overline{x}` = Sample mean

z* = critical z-value.

`\sigma` = Population standard deviation.

n= Sample size.

Let x be the denotes the monthly rent for unfurnished one bedroom apartments available for rent in this community.

As per given , we have

n= 10

`\overline{x}=\$580`

`\sigma=\$90`

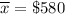
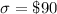
Critical value for 95% confidence : z* = 1.96

So the 95% confidence interval becomes,

`580\pm (1.96) (90)/(√(10))`

`=580\pm (1.96) (90)/(3.162278)`

`=580\pm (1.96)(28.46)`

`=580\pm 55.78`

`=(580-55.78,\ 580+55.78)=(524.22,\ 635.78)`

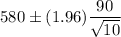
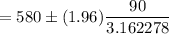
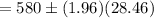
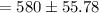
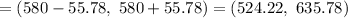
Hence, a 95% confidence interval for the mean monthly rent for unfurnished one bedroom apartments available for rent in this community=
`(\$524.22,\ \$635.78)`