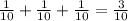Answer:
a. 720
b. 0.3
Explanation:
a.
Three balls are selected at random without replacement.
First ball can be selected in 10 ways
Second ball can be selected in 9 ways
Third ball can be selected in 8 ways
Thus, there are 10×9×8 =720 different ways of selecting three balls.
b.
There are three cases that satisfy this condition
- first ball picked is 5, the others are not
- first ball is not 5, second is 5, third is not
- first and second ball is not five, third ball is 5
Each probabilities are:
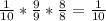

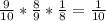
Thus, one of the balls selected is the number 5 is then