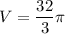Question

Find the volume of the largest circular cone that can
beinscribed in a shpere of radius 3.

Answer 1

`V =(32)/(3)\pi`

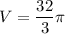
Explanation:

given,

radius of sphere = 3

volume of cone:

`V = (1)/(3)\pi r^2h`

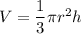
r is the radius of circular base

h is the height of the cone

here r = x and h = 3 + y

now, volume in term of x and y

`V = (1)/(3)\pi x^2(3+y)`

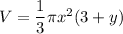
Applying Pythagoras theorem

x² + y² = 3²

`x = √(9-y^2)`

`V = (1)/(3)\pi ( √(9-y^2))^2(3+y)`

`V = (1)/(3)\pi ( 9-y^2)(3+y)`

`V = (1)/(3)\pi (27 + 9 y - 3 y^2-y^3)`

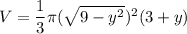
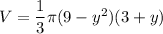
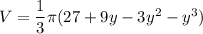
differentiating both side

`(dV)/(dy) =(1)/(3)\pi ( 9-6y- 3y^2)`

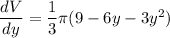
for maxima
`(dV)/(dy) = 0`

`\pi ( 3-2 y - y^2)=0`

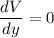
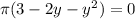
y² + 2 y - 3 = 0

(y+3)(y-1)=0

y = 1,-3

y cannot be negative so, volume at y = 1

`V = (1)/(3)\pi (27 + 9 (1)- 3(1)^2-(1)^3)`

`V =(32)/(3)\pi`

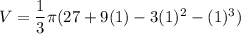
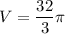
Hence, the largest cone which can be inscribed in the spheres of the radius 3 has volume
`V =(32)/(3)\pi`