Question

8. For many computer tablets, the owner can set a 4-digit pass code to lock the device.

a. How many different 4-digit pass codes are possible if the digits cannot be repeated? How did you get your answer?
b. If the digits of a pass code are chosen at random and without replacement from the digits 0, 1, … , 9, what is the probability that the pass code is 1234? How did you get your answer?
c. What is the probability that two people, who both chose a pass code by selecting digits at random and without replacement, both have a pass code of 1234? Explain your answer.

Answer 1

a. There 5040 different pass codes if the digits cannot be repeated

b. The probability that the pass code is 1234 is ≈ 0.0002

c. The probability that two people both have a pass code of 1234 is 4×
`10^(-8)`

Explanation:

a. How many different 4-digit pass codes are possible if the digits cannot be repeated?

There are

• 10 possibilities for the first digit

• 9 possibilities for the second digit

• 8 possibilities for the third digit

• 7 possibilities for the fourth digit

Thus there are 10×9×8×7=5040 different pass codes

b. If the digits of a pass code are chosen at random and without replacement from the digits, what is the probability that the pass code is 1234

The probability that the first digit is 1 is
`(1)/(10)`

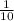
The probability that the second digit is 2 is
`(1)/(9)`

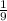
The probability that the second digit is 3 is
`(1)/(8)`

The probability that the fourth digit is 4 is
`(1)/(7)`

Thus the probability that the pass code is 1234 is
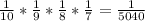`(1)/(10) * (1)/(9) *(1)/(8) *(1)/(7) =(1)/(5040)` ≈ 0.0002

c. The probability that two people, who both chose a pass code by selecting digits at random and without replacement, both have a pass code of 1234?

The probability that the pass code of the one person is 1234 is 0.0002

The probability that the pass code of the other person is 1234 is 0.0002

Thus, the probability that two people have both pass code of 1234 is

0.0002×0.0002 = 4×
`10^(-8)`