Question

Find the limit of the following sequence or determine that the limit does not exist. {5n/Squareroot 81 n^2 + 5} Select the correct choice below and, if necessary, fill in the answer box to complete your choice.

A. The sequence is monotonic, but it is unbounded. The limit is_________---
B. The sequence is not monotonic, but it is bounded. The limit is_____________
C. The sequence is monotonic and bounded. The limit is____________
D. The sequence is monotonic, unbounded, and the limit does not exist.

Answer 1

C. The sequence is monotonic and bounded. The limit is 5/9

Explanation:

For this case we have the following n term:

`a_n = (5n)/(√(81n^2 +5))`

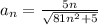
And we can find the limit when x tend to infinity:

`\lim_(n\to\infty) (5n)/(√(81n^2 +5))`

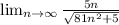
And we got this:

`5 \lim_(n\to\infty) (n)/(√(81n^2 +5))`

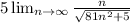
Now we can divide by n the numerator and denominator like this:

`5 \lim_(n\to\infty) \frac{1}{\sqrt{81 +(5)/(n^2)}}`

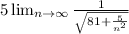
And now we can apply properties of limits and we got this:

`5 \frac{\lim_(n\to\infty) 1}{\lim_(n\to\infty) \sqrt{81 +(5)/(n^2)}}`

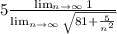
And we got:

`5 (1)/(9)=(5)/(9)`

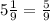
So then our sequence is bounded by
`(5)/(9)`

By definition a monotonic sequence is a "sequence that is always increasing or decreasing".

For this case if we find:

`a_1 = (5)/(√(86))`

`a_2 = (10)/(√(329))`

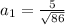
We see that
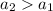`a_2 >a_1` and in general we see that
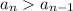`a_n >a_(n-1)`. So then the ebst answer for this case is:

C. The sequence is monotonic and bounded. The limit is 5/9