Question

Prove that if B=(P,P,...,P) is any subset of a linear space L, then M=Span B is a subspace of L.

Answer 1

See the proof below.

Explanation:

We can proof this with the following theorem "Let B a subset of a vector space of L then the span(B) is a subspace of L , and is the samlles subspace containing B"

Proof

We can show that the span(B) is a subspace of L.

For this special case we assume that
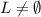`L \\eq \emptyset` and for this case the
`span(B) \\eq \emptyset` and we can see that B \subseteq M=span (B) [/tex]

In order to see that the span(B) is a subspace of L we can assume two elements let's say
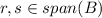`r,s \in span(B)` we can write this like that:

`r= a_1 r_1 + ...+a_n r_n`

`s = b_1 s_1 + ...+ b_m s_m`

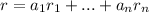
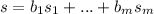
For some vectors
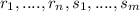`r_1,....,r_n , s_1,....,s_m` \in B and scalars
`a_1,...,a_n , b_1,....,b_m` in R

So then the linear combination r+s is defined as:

`r+s = a_1 r_1 +...+ a_n r_n + b_1 s_1 + ...+b_m s_m \in M=span(B)`

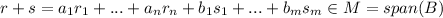
Let
`\alpha` a constant in R

`\alpha r = \alpha a_1 r_1 + ....+ \alpha a_n r_s \in M=span(B)`

`\alpha s = \alpha b_1 s_1 + ....+ \alpha b_m s_m \in M=span(B)`

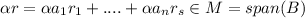
So then we have all the conditions satisifed and we can conclude that M=span(B) is a subspace of L.