Question

9. Consider the circles with the following equations:

x^2+y^2=2 and
(x−3)^2+(y−3)^2=32.
a. What are the radii of the two circles?
b. What is the distance between their centers?
c. Make a rough sketch of the two circles to explain why the circles must be tangent to one another.

Answer 1

Answer with Step-by-step explanation:

We are given that

`x^2+y^2=(\sqrt 2)^2`

`(x-3)^2+(y-3)^2=32=(4\sqrt 2)^2`

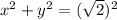
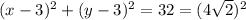
Compare with the equation of circle

`(x-h)^2+(y-k)^2=r^2`

Where center of circle=(h,k)

r=Radius of circle

a.Center of circle=(0,0)

Radius=
`\sqrt 2` units

Center of second circle=(3,3)

Radius of second circle=
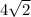`4\sqrt 2` units

b.Distance formula:
`\sqrt{(x_2-x_1)^2+(y_2-y_1)^2`

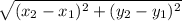
Using the formula

The distance between the centers of two circle

=
`√((3-0)^2+(3-0)^2)=3\sqrt 2`

Hence, the distance between the centers of two circle =
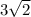`3\sqrt 2` units.

c.

Substitute x=-1 and -1

`1+1=2=`

`(1-3)^2+(1-3)^2=32`

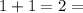
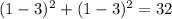
The circle must be tangent because there is just one point (-1,-1) is common in both circles and satisfied the equations of circle.