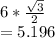Question

9. The radius of a circle is 6.

a. If the angle formed between two tangent lines to the circle is 60°, how long are the segments between the point of intersection of the tangent lines and the circle?.
b. If the angle formed between the two tangent lines is 120°, how long are each of the segments between the point of intersection of the tangent lines and the point of tangency?
Round to the nearest hundredth

Answer 1

12,5.196

Explanation:

given that the radius of a circle is 6.

We have any tangent drawn from outside point there will be two tangents of equal length and also the line joining point of intersection of tangent with centre of circle will bisect the angle between the tangents.

When angle between the two tangents is 60, we have the right triangle formed by radius, one tangent, and line joining point of intersection of tangent with centre of circle with angles 30,60 and 90

Hence the hypotenuse = length of line segment of tangent = 2 (radius) = 12

Part 2:

When angle between tangents is 120, we have 60,30,90 right triangle and hence length of tangent = radius * sin 60

=
`6*(√(3) )/(2) \\=5.196`