Answer with Step-by-step explanation:
We are given that a line passing through the point (p-4,2) and (-2,9) and other line passing through the point (p,-1) and (-1,1).
Slope-formula:

By using the formula
Slope of line which passing through the point (p-4,2) and (-2,9)

Slope of other line which passing through the point (p,-1) and (-1,1)
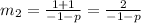
When two lines are parallel then their slopes are equal
a.


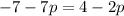
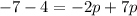
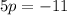
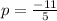
b.If the two lines are perpendicular then their slopes is opposite reciprocal to each other.
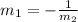
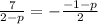
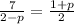
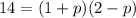
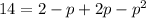
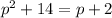
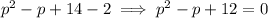
It is quadratic equation in variable p
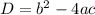
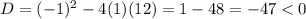
The root of equation are imaginary which is not possible .
If the lines are perpendicular then the value of p does not exist.