Answer:
See explanation and proof below.
Explanation:
For this case we want to proof the following:
"Given that V is a finite dimensional and
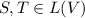 then ST is invertible if and only if S and T are both invertible.
then ST is invertible if and only if S and T are both invertible.
In order to proof this we need to use the following result :"Given a finite dimensional vector space V, for any T \in L(V,V) we have the following properties defined: "invertibility, surjectivity, injectivity".
Proof
(> statement)
For the first part of the proof we can do this. We assume
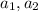 two vectors in V. If we assume that ST is invertible and
two vectors in V. If we assume that ST is invertible and
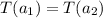 then we have this :
then we have this :
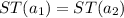
And since ST is invertible then
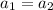 and that implies that T is invertible.
and that implies that T is invertible.
Now if we select a vector b in V , since we know that ST is invertible, and by the surjective property defined above we have that for any
 then
then
 and we see that
and we see that
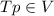 and S is surjective and by the result above is invertible.
and S is surjective and by the result above is invertible.
(< statement)
Now for this part we can assume that S and T are invertible and then
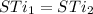 for any two vectors
for any two vectors
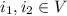 . Since S,T are invertible and using the surjective property we have that for any vectors
. Since S,T are invertible and using the surjective property we have that for any vectors
 we have that:
we have that:
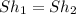
And since
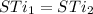 and because S satisfy the injectivity property that implies:
and because S satisfy the injectivity property that implies:
 and we can conclude that
and we can conclude that
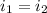 and the conclusion is that ST is injective and invertible for this case.
and the conclusion is that ST is injective and invertible for this case.
And with that we complete the proof.